Nanoindentation Automated Analysis Example
We have defined some metrics for good analyses previously post. This method still requires some manual selection to remove clusters of analyses that produce bad analyses.
Baseline Analysis
- segment size (10:5:400)
- overlap requirement low (>10%)
- R2 for zero point low (>0.5)
- Modulus must be real
- No judgment on quality of stress-strain curve
Analysis Work Flow
- iterate through segments with the three linear fits saving only necessary variables for filtering
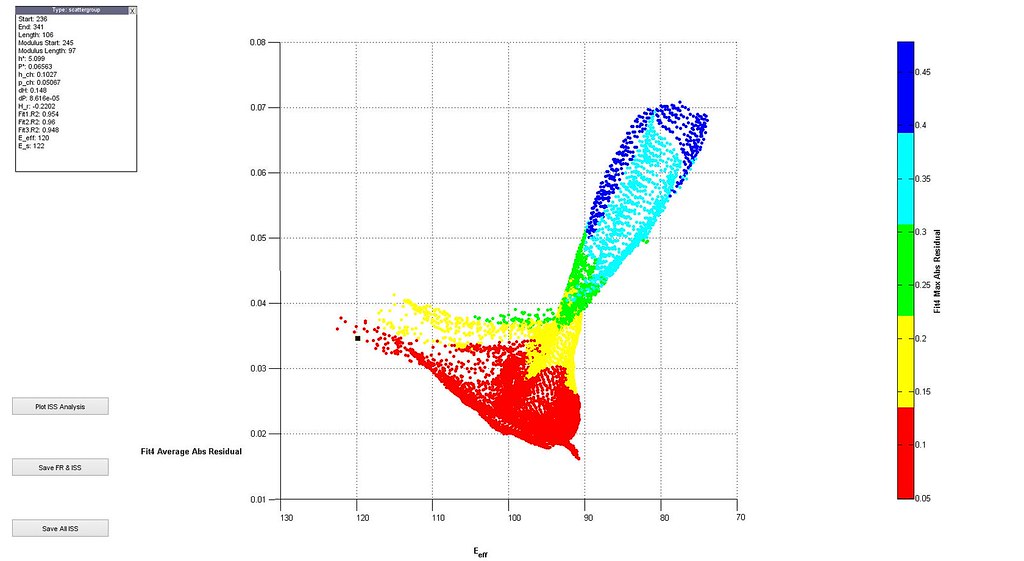
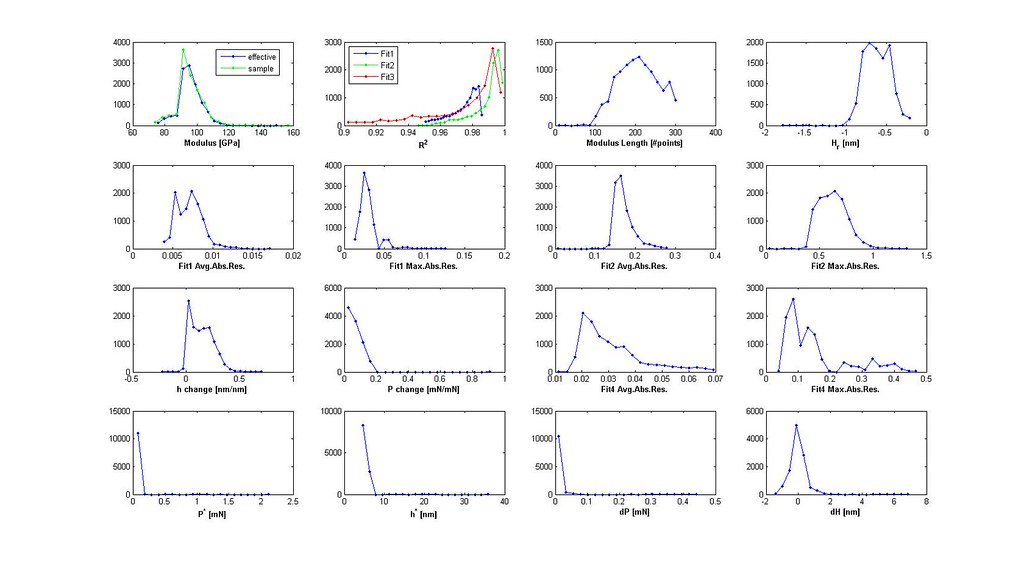
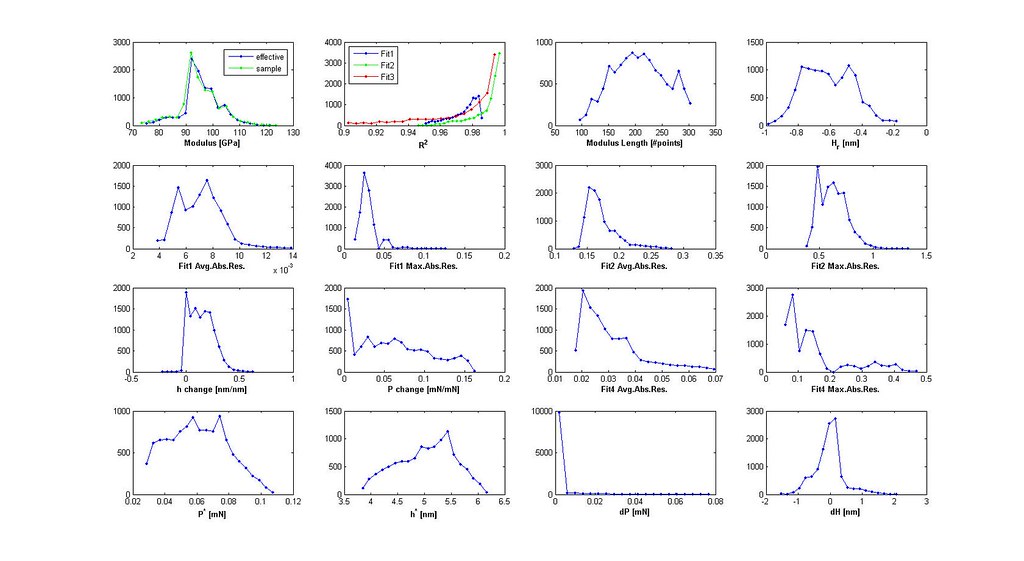
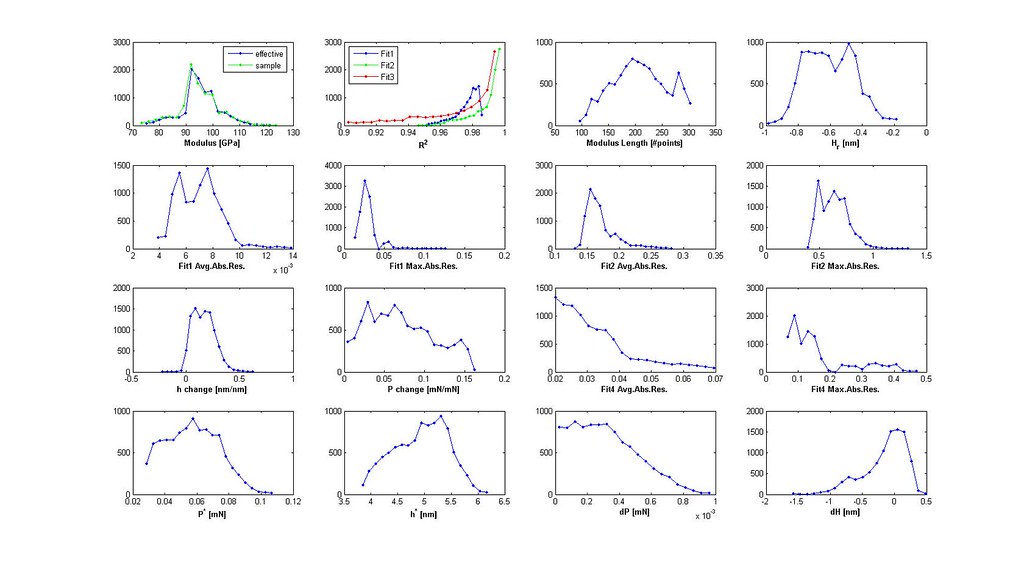
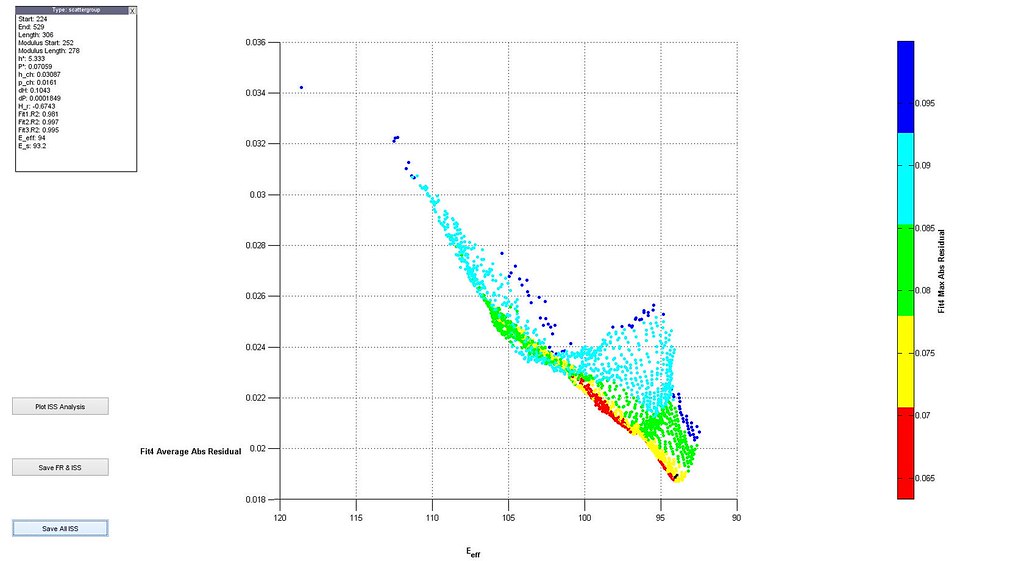
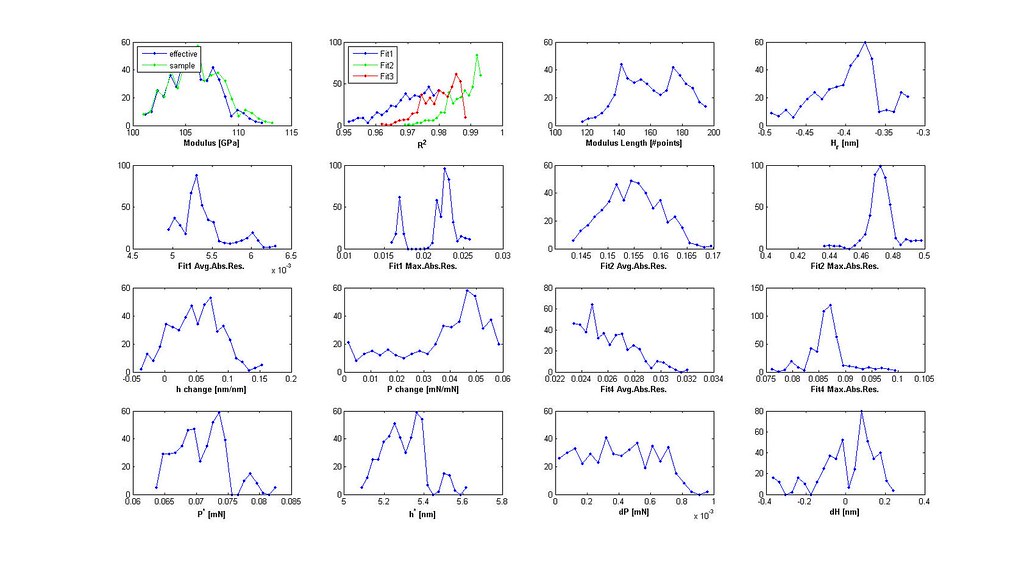
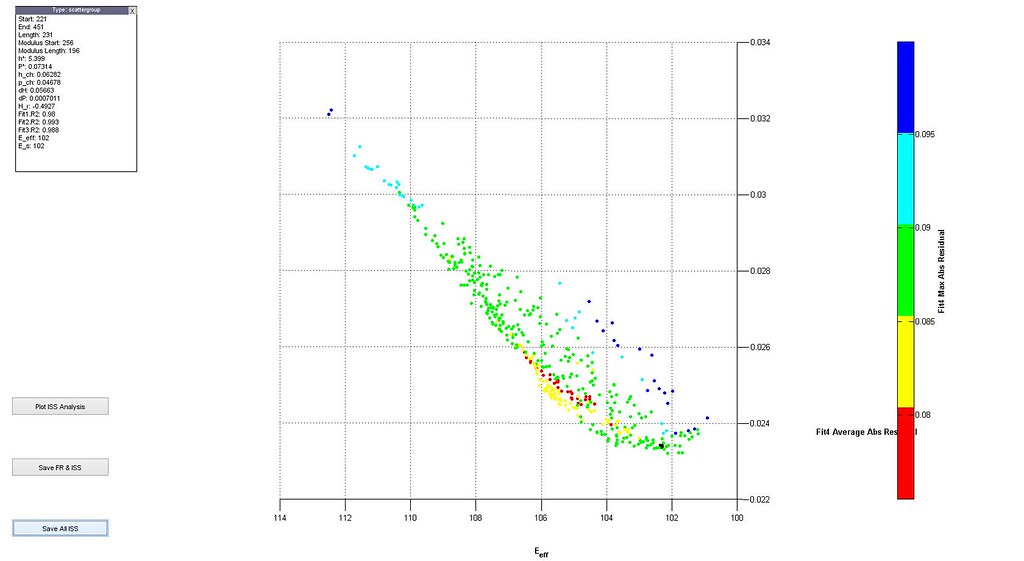
- plot distributions 3D scatter plot of filtered analyses
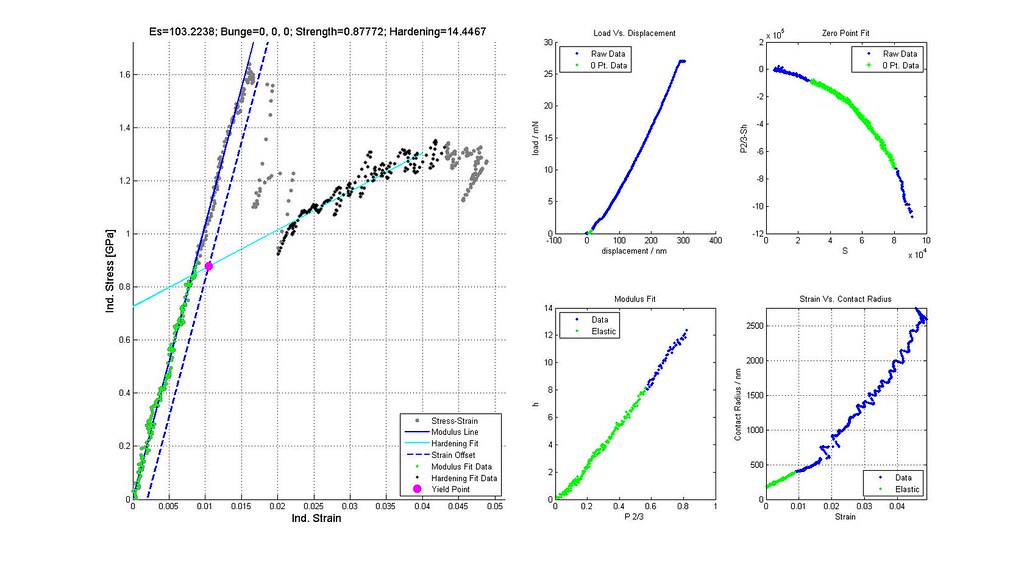
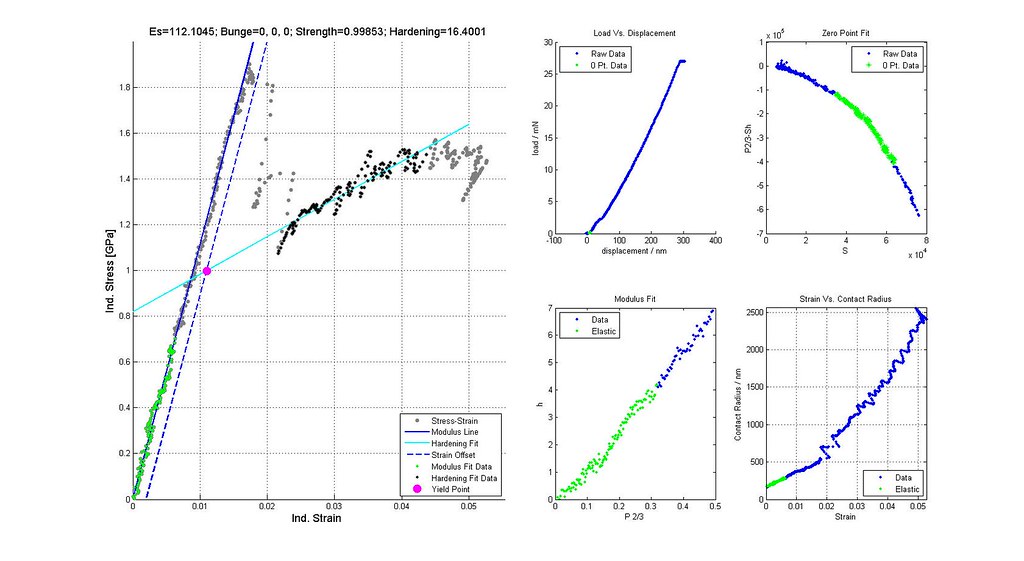
- plot stress-strain curves of a few selected analyses particularly at the boundaries of the scatter plot
- iterate through filtering using the distributions and 3D scatter plot to determine cutoffs until the majority of the stress-strain curves are acceptable
- calculate stress-strain and plastic properties for all acceptable analyses
- verify yield strengths are correctly determined from offset or back extrapolated
- calculate the statistics of the modulus, yield strength, and hardening
- save work space
Case Study
Sample is CPTi, 16um indenter radius, 2014-02-26 Batch #00002. 892 data points. 32,378 Analyses.
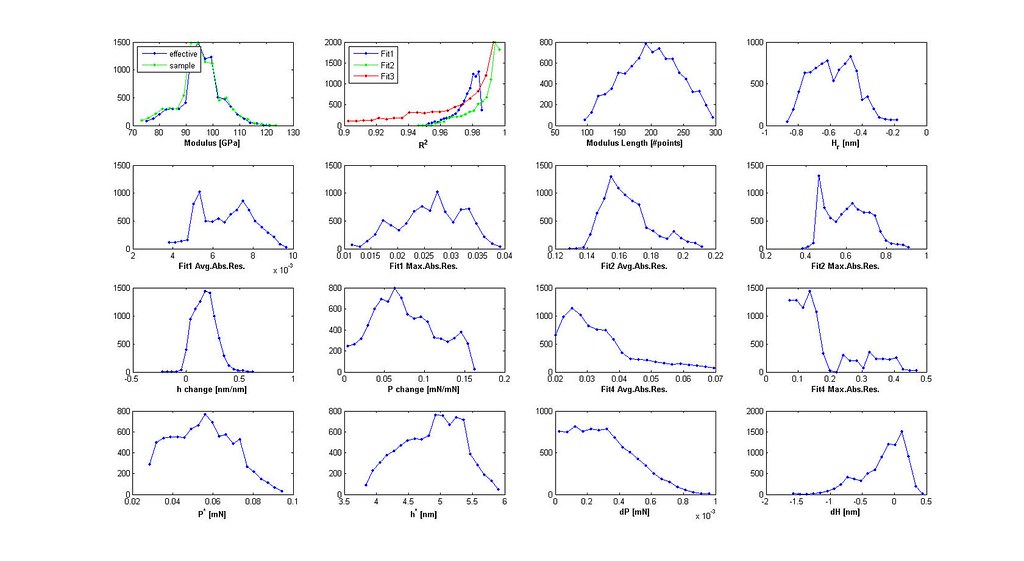
Iteration 1
Filt ={ 'Modulus', [1000 10]}
Iteration 2
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90}
Iteration 3
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100}
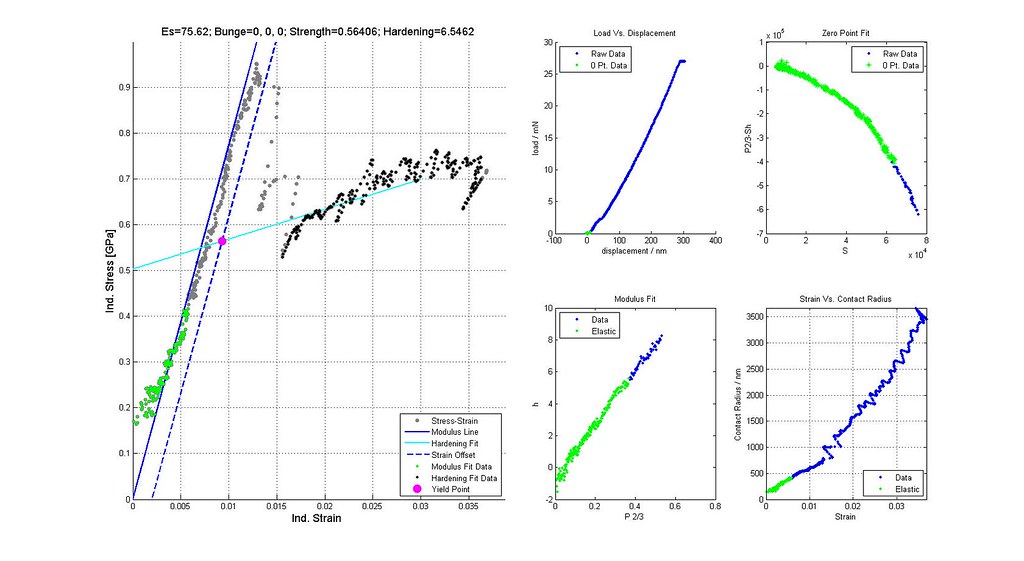
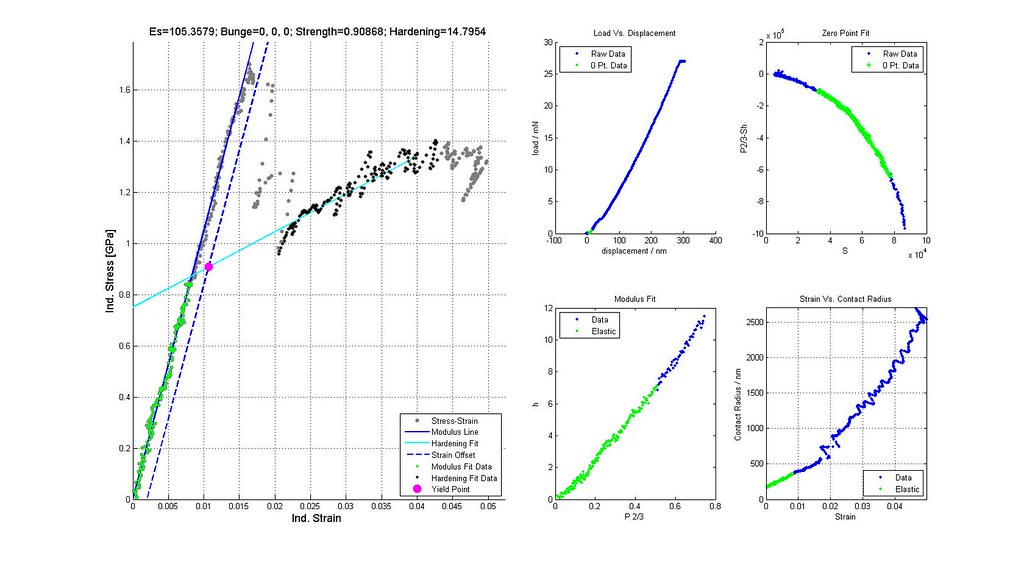
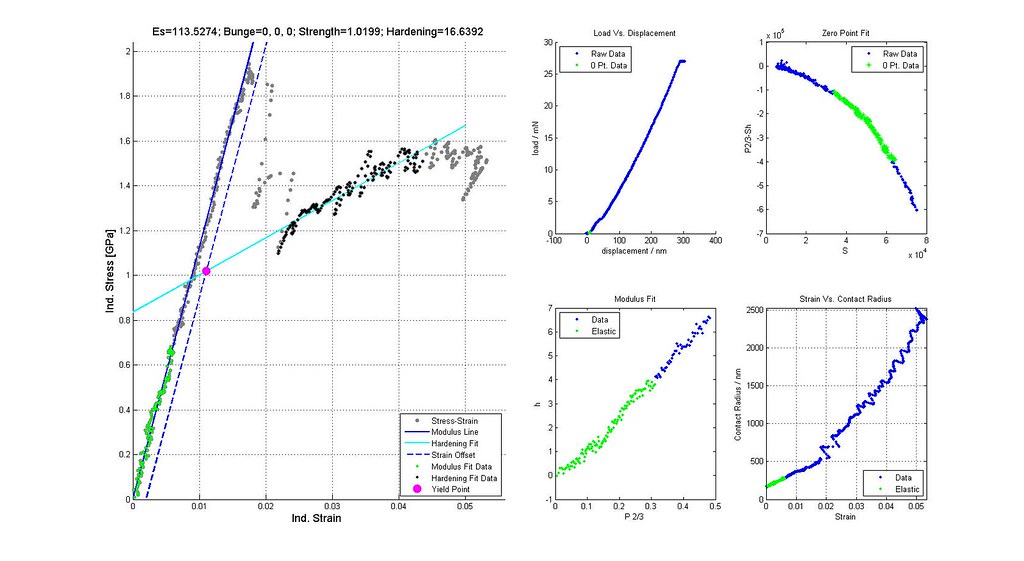
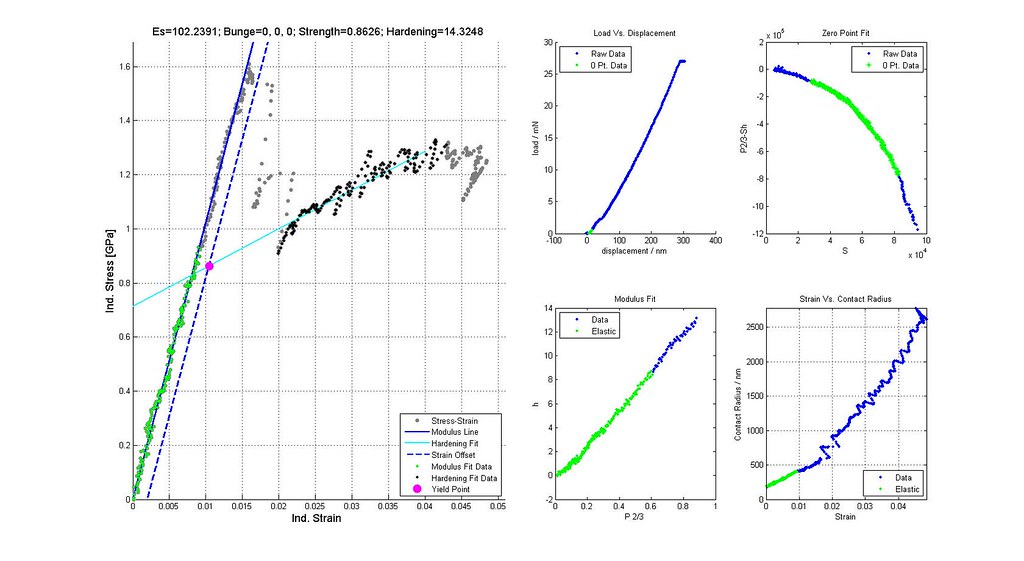
Saved Search Scatter Plot and Example Stress-Strain Curves
Iteration 4
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001}
Iteration 5
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04}
Iteration 6
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04; 'MAR4', 0.1}
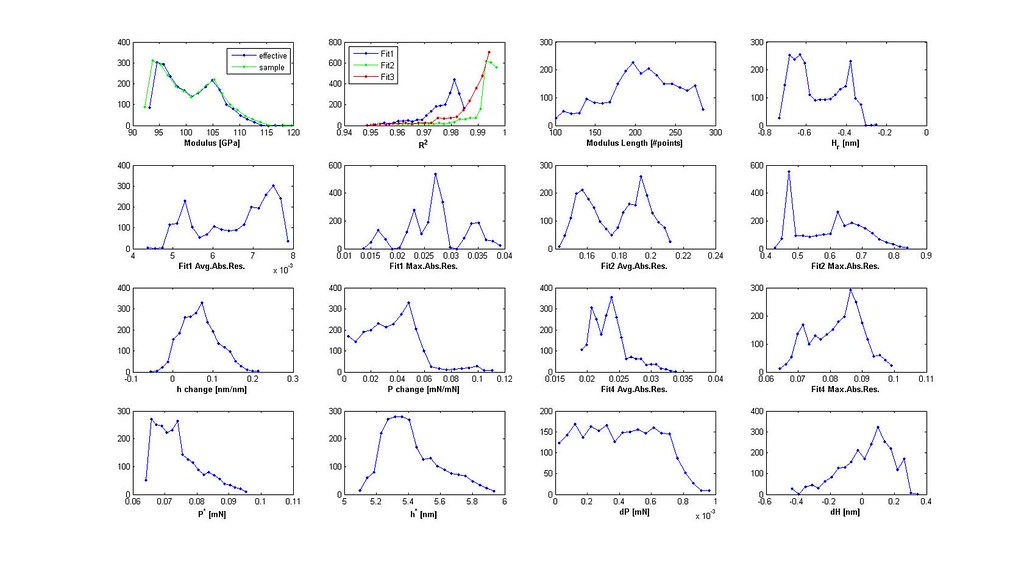
Iteration 7
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04; 'MAR4', 0.1; 'p_change', [0.06 0]}
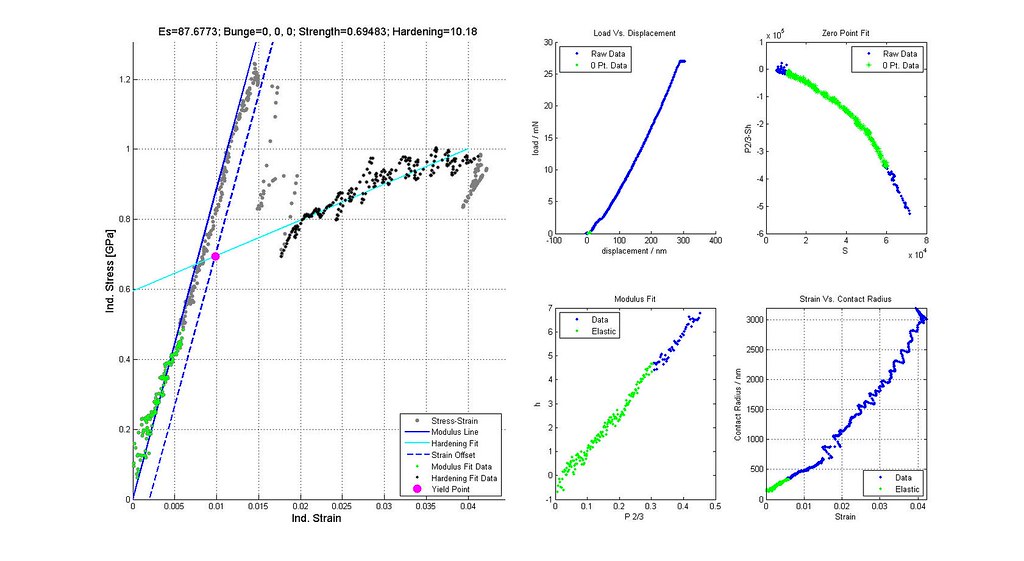
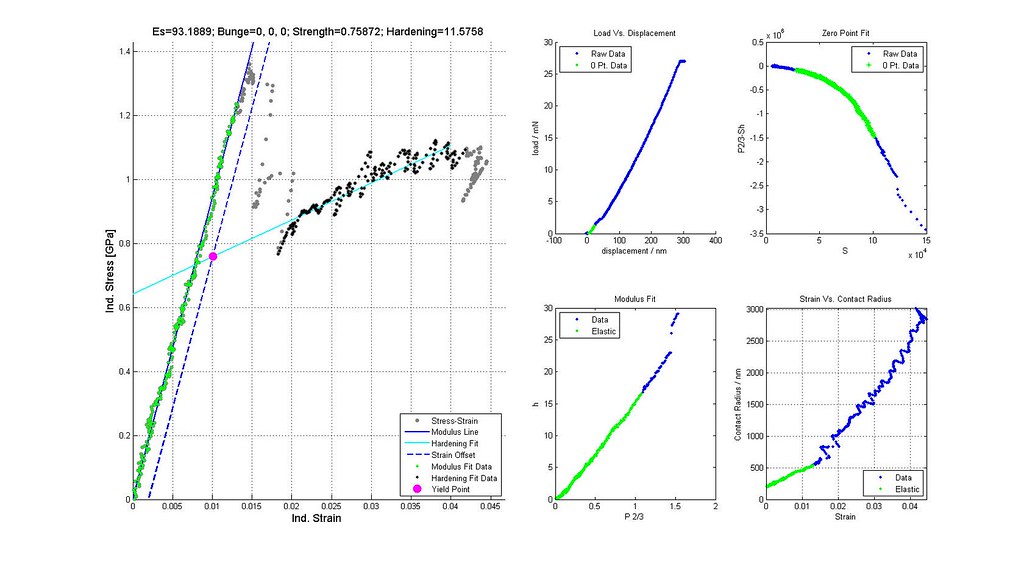
 Saved Search Scatter Plot and Example Stress-Strain Curves
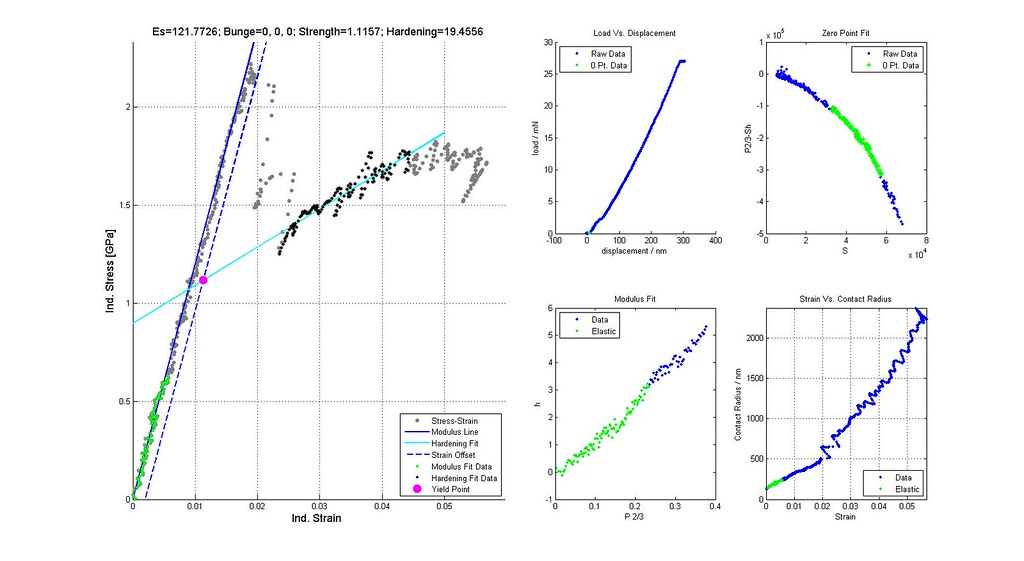
Saved Search Scatter Plot and Example Stress-Strain Curves
Saved all Stress-Strain Data
Estat =
mean: 100.0200
median: 99.2786
stdev: 4.6270
min: 92.4900
max: 118.6119
Ystat =
mean: 0.8365
median: 0.8220
stdev: 0.0610
min: 0.7394
max: 1.0960
Hstat =
mean: 13.4397
median: 13.3776
stdev: 1.4401
min: 11.1772
max: 19.1546
Iteration 8
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04; 'MAR4', 0.1; 'p_change', [0.06 0]; 'MAR2', 0.5}
Iteration 9
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04; 'MAR4', 0.1; 'p_change', [0.06 0]; 'MAR2', 0.5; 'Hr', [-0.3 -0.5]}
Saved Search Scatter Plot and Example Stress-Strain Curves
Saved all Stress-Strain Data
Estat =
mean: 105.8270
median: 105.7222
stdev: 2.2997
min: 100.9116
max: 112.5039
Ystat =
mean: 0.9153
median: 0.9173
stdev: 0.0325
min: 0.8437
max: 1.0199
Hstat =
mean: 15.1464
median: 14.9451
stdev: 0.6875
min: 13.9577
max: 16.6392
Iteration 10
Filt ={ 'Modulus', [1000 10]; 'R21', 0.95; 'R22', 0.90; 'R23', 0.90; 'P*', 0.1100; 'dP', 0.001; 'MAR1', 0.04; 'MAR4', 0.09; 'p_change', [0.06 0]; 'MAR2', 0.49}
Saved all Stress-Strain Data
Estat =
mean: 105.2801
median: 105.5839
stdev: 2.4332
min: 99.7603
max: 110.0666
Ystat =
mean: 0.9071
median: 0.9156
stdev: 0.0338
min: 0.8320
max: 0.9784
Hstat =
mean: 15.0195
median: 14.8722
stdev: 0.7281
min: 13.4207
max: 16.2188
Progression of number of good analyses based on Filt variables for 10th iteration of Filt.
npoints =
32378
32353
13270
12875
11073
11029
9651
8721
2051
2025
434
There is not much more reasoning in filtering the data further
note: Images labeled 6 and 8 are actually for iterations 7 and 9 and correctly positioned in this post. The orientation of the grain where the indent was run is not (0,0,0)
The matlab code and data used for this analysis can be found here: code and data