Introduction

The elastic stiffness tensor for different orientations from the Hexagonal-Triclinic fundamental zone may be identical. This non-uniqueness may be a result of both the definition of Bunge Euler angles and the elastic properties of crystals with Hexagonal symmetry. In this post we find which orientations have the same elastic stiffness tensors so that we may more efficiently select orientations for calibration in the Materials Knowledge System.

Procedure

Orientations were selected from Hexagonal-Triclinic fundamental zone ($ 0 \leq \phi_1 \leq 2\pi, 0 \leq \Phi < \frac{\pi}{2}, 0 \leq \phi_2 \leq \frac{\pi}{3} $).

Orienatations were selected to reside in bins of equal size in orientation space. The orientation invariant measure of orientation space can be written as follows, $dg = sin(\Phi) d\phi_1 d\Phi d\phi_2$. While the increments in $\phi_1$ and $\phi_2$ may be independent of the angles themselves, the size of the $\Phi$ increment must increase as $\Phi$ approaches zero to ensure that the orientation bins are equal in size. It can be found that equal orientation bins may be generated by the spacing $dg_{\Phi} = acos(x)$ where $x$ increments equally between 0 and 1.

Once the orientations were selected the elastic stiffness tensor for each in the sample configuration were calculated (X.Wu 2007).

# -*- coding: utf-8 -*-
"""
Created on Thu Nov 13 09:52:43 2014

The following python code generates the elastic stiffness tensor and matrix
for a single hexagonal crystal given Bunge-Euler angles and the relevant
elastic stiffness constants in the reference frame.

@author: nhpnp3
"""

import numpy as np

def stiffness_calc(phi):
## phi: vector of bunge euler angles [phi1,Phi,phi2]
## Cs: 3x3x3x3 stiffness tensor
## CsM: 6x6 stiffness matrix
  
  # These are the Elastic Stiffness Constants
  C11 = 154
  C12 = 86
  C13 = 67
  C33 = 183
  C44 = 46
  
      
  z1 = np.array([[    np.cos(phi[0]), np.sin(phi[0]), 0],
                 [ -1*np.sin(phi[0]), np.cos(phi[0]), 0],
                 [                 0,              0, 1]])
  
  x = np.array([[ 1,                 0,              0],
                 [ 0,    np.cos(phi[1]), np.sin(phi[1])],
                 [ 0, -1*np.sin(phi[1]), np.cos(phi[1])]])
                
 z2 = np.array([[    np.cos(phi[2]), np.sin(phi[2]), 0],
                 [ -1*np.sin(phi[2]), np.cos(phi[2]), 0],
                 [                 0,              0, 1]])
                 
  
  g = np.dot(z1,np.dot(x,z2)) # transformation matrix from crystal to sample
  
  Cs = np.zeros([3,3,3,3])
  
  for cc in xrange(3**4):
      [ii,jj,kk,ll] = np.unravel_index(cc,[3,3,3,3])
      
  
      A1 = 0    
      for tt in xrange(3):    
          A1 += g[ii,tt]*g[jj,tt]*g[kk,tt]*g[ll,tt] 
      
      A2 = 0.5*(g[ii,0]*g[jj,1]*g[kk,0]*g[ll,1]
              + g[ii,0]*g[jj,1]*g[kk,1]*g[ll,0]
              + g[ii,1]*g[jj,0]*g[kk,0]*g[ll,1]
              + g[ii,1]*g[jj,0]*g[kk,1]*g[ll,0])    
      
      A =  A1 + A2 
      
      B = 0
      
      for tt in xrange(2):
          B += g[ii,tt]*g[jj,tt]*g[kk,2]*g[ll,2]
          + g[ii,2]*g[jj,2]*g[kk,tt]*g[ll,tt]
  
      D = g[ii,2]*g[jj,2]*g[kk,2]*g[ll,2]    
      
      Cs[ii,jj,kk,ll] = C12 * int(ii==jj) * int(kk==ll) + C44 * (int(ii==kk) * \
                        int(jj==ll) + int(ii==ll) * int(kk==jj)) + (C11 - C12 -
                        2*C44) * A + (C13 - C12) * B + (C33 - C11) * D
  
  
  CsM = np.array([[Cs[0,0,0,0],Cs[0,0,1,1],Cs[0,0,2,2],Cs[0,0,1,2],Cs[0,0,0,2],Cs[0,0,0,1]],
                  [Cs[0,0,1,1],Cs[1,1,1,1],Cs[1,1,2,2],Cs[1,1,1,2],Cs[1,1,0,2],Cs[1,1,0,1]],
                  [Cs[0,0,2,2],Cs[1,1,2,2],Cs[2,2,2,2],Cs[2,2,1,2],Cs[2,2,0,2],Cs[2,2,0,1]],
                  [Cs[0,0,1,2],Cs[1,1,1,2],Cs[2,2,1,2],Cs[1,2,1,2],Cs[1,2,0,2],Cs[1,2,0,1]],
                  [Cs[0,0,0,2],Cs[1,1,0,2],Cs[2,2,0,2],Cs[1,2,0,2],Cs[0,2,0,2],Cs[0,2,0,1]],
                  [Cs[0,0,0,1],Cs[1,1,0,1],Cs[2,2,0,1],Cs[1,2,0,1],Cs[0,2,0,1],Cs[0,1,0,1]]])
                  
  return Cs, CsM

Lastly, the stiffness matrices were compared for every combination of orienations and these results were plotted.

Results

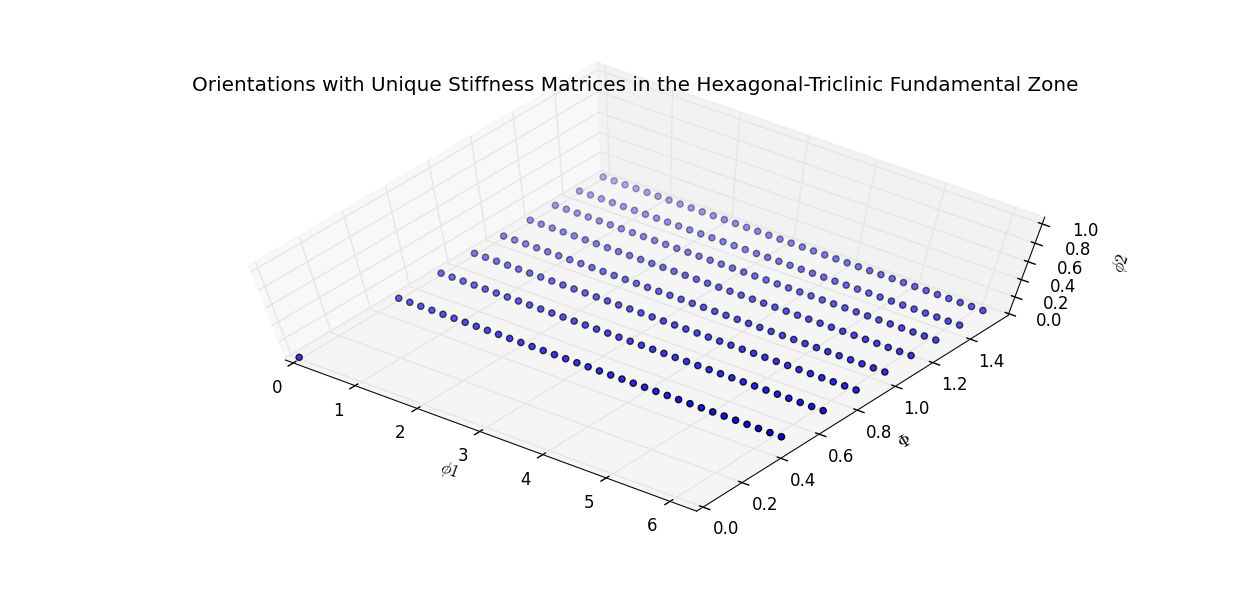
The following two images show which orientations in the Hexagonal-Triclinic fundamental zone have identical elastic stiffness tensors.

in the following image orientations with the same elastic stiffness tensors are shown with the same marker color

the following image shows a selection of unique orientations in the Hexagonal-Triclinic fundamental zone

The following observations are made from the preceding images:

  1. The stiffness tensor is independent of the $\phi_2$ angle
  2. The stiffness tensors are identical for all orientations on the $\Phi = 0$ face
  3. The stiffness tensors are identical when $\phi_1 = 0$ degrees and $\phi_1 = 360$ degrees if the $\Phi$ angles are the same.

References

  • http://neon.mems.cmu.edu/rollett/27750/27750.html

  • X. Wu, G. Proust, M. Knezevic, S.R. Kalidindi Elastic-plastic property closures for hexagonal close-packed polycrystalline metals using first-order bounding theories Acta Mater, 55(2007) Volume 55, p. 2729