Plotting GSH Coefficients for Orientations in the Hexagonal-Triclinic Fundamental Zone
Introduction
In a previous study it was shown that orientations on the exterior of the cubic-triclinic fundamental zone in Euler space completely bound the interior points in both Euler and GSH space. This post investigates whether this is also the case for GSH coefficients up to a truncation level of L = 4 for hexagonal-triclinic symmetry.
Procedure
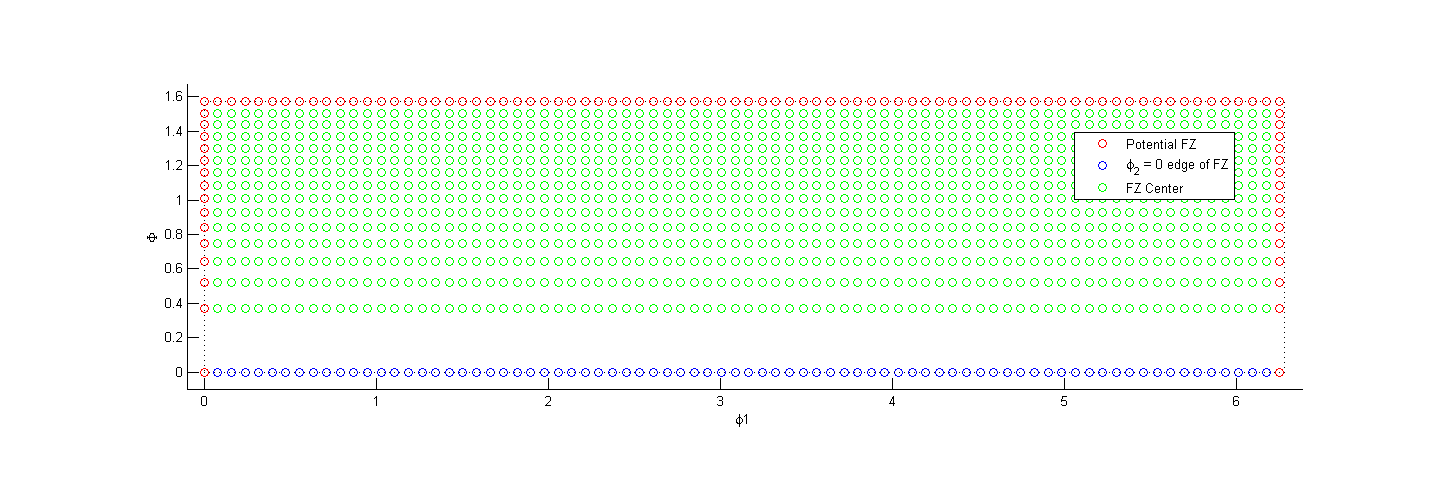
The first step was to select a set of orientations from the hexagonal-triclinic fundamental zone to plot in GSH coefficient space. While the entire hexagonal-triclinic fundamental zone covers $ 0 \leq \phi_1 \leq 2\pi, 0 \leq \Phi < \frac{\pi}{2}, 0 \leq \phi_2 \leq \frac{\pi}{3} $, only orientations in the $ \phi_2 = 0 $ face were used as $ \phi_2 $ has no influence on the GSH coefficients at the L = 4 truncation level.
the following plot shows the orientations selected for this effort
Notice that the interior points in this face are colored green while the exterior is red (the $ \Phi = 0 $ edge points are blue, and all have identical orientations in Bunge Euler angles). For an explanation of the spacing in the selection of points along the $ \Phi $ axis see the following post.
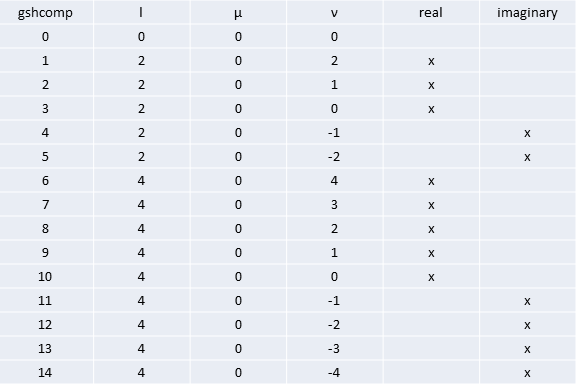
Next, the GSH coefficients for each set of Euler angles were calculated. Since most of the coefficients are complex, they were each split into their real and imaginary parts so that they could be visualized. Due to symmetry inherent in the coefficients certain real/imaginary parts could be ignored.
the following chart shows which real and imaginary parts were selected from each coefficient and the label they were given
Finally, the components were plotted against each other in both 2-D and 3-D.
Results
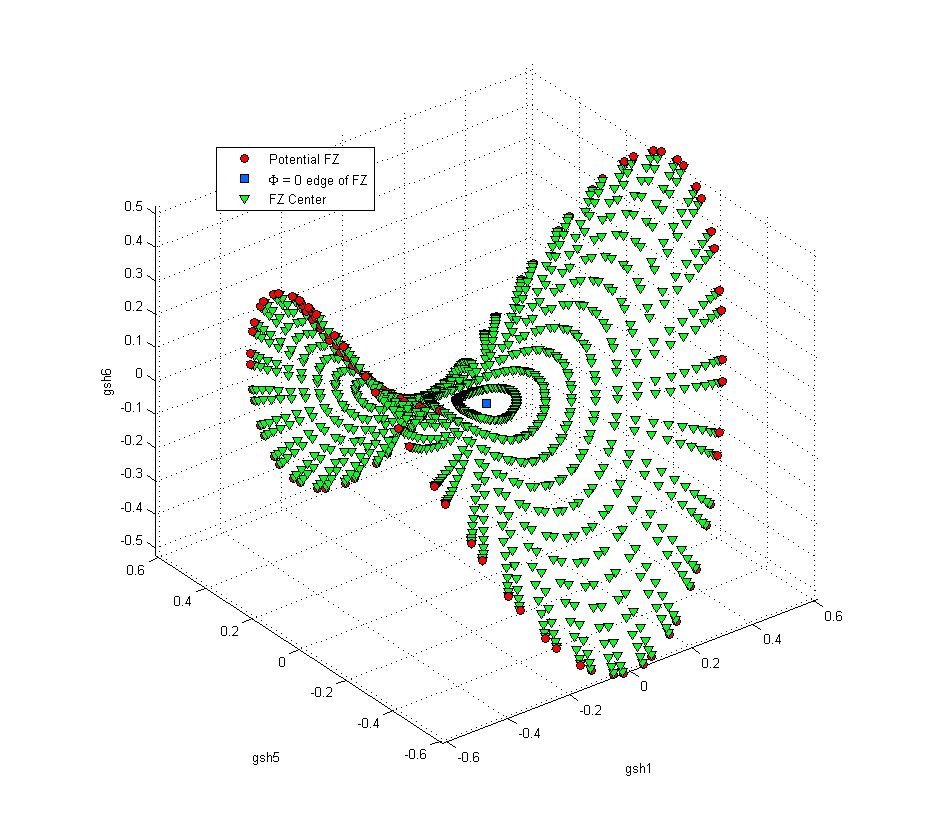
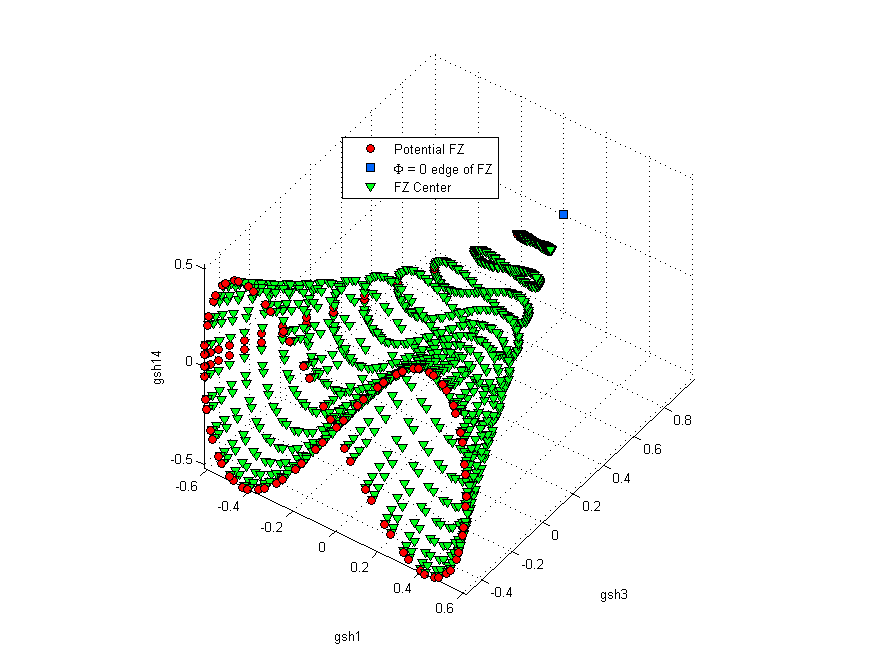
In the following two images, sections of the GSH coefficients of the original orientations are plotted in 3-D
In the following gallery the first GSH coefficient is plotted against the other 13 coefficients in 2-D
Conclusions
From these images it is clear that the exterior points of the $ \phi_2 = 0 $ face of the hexagonal-triclinic fundamental zone in no way bound the interior points for a truncation level of L = 4. This indicates that it is necessary to use the entire face (sans the non-uniqueness inherent in the definition of Bunge Euler angles) in the calibration of the MKS to achieve the most accurate possible results.
References
- X. Wu, G. Proust, M. Knezevic, S.R. Kalidindi Elastic-plastic property closures for hexagonal close-packed polycrystalline metals using first-order bounding theories Acta Mater, 55(2007) Volume 55, p. 2729